オリオン形而上学研究所 » 白銀比・黄金比の幾何学

研究分野

私は４年ほど前より、数学上の特別な比である黄金比、白銀比、黄金二乗比、白銀二乗比に焦点を当てた幾何学分野の研究をしています。これらは白銀二乗比以外全て無理数で、その小数点以下４桁までの値は、下記のとおりです。

黄金比——– 1 : 1.6180

白銀比——– 1 : 1.4142

黄金二乗比— 1 : 2.6180

白銀二乗比— 1 : 2.0000

黄金二乗比は黄金比の二乗であり、その小数点以下の数字は黄金比と全く同じです。また、白銀二乗比は白銀比の二乗です。そして、黄金菱形、白銀菱形、黄金二乗菱形、白銀二乗菱形とは、それぞれ、対角線の長さの比が黄金比、白銀比、黄金二乗比、白銀二乗比になる菱形のことです。また、白銀二乗長方形、黄金長方形とは、それぞれ、２辺の長さの比が白銀二乗比、黄金比である長方形のことです。

これらの研究を進める上で、佐藤郁郎先生、一松信先生、宮崎興二先生、渡辺泰成先生、秋山仁先生からいろいろとアドバイスを頂いており、これが私の研究を進める上で大変助けになっています。特に佐藤先生は、新たに創作された多面体の二面角の計算を含む、時間のかかるサポートをして下さっています。あらためて諸先生方に心からお礼申し上げます。また、多面体木工の達人であり、『積み木インテリアギャラリー』を主宰されている中川宏さんにも、常日頃お世話になっています。ちなみに、右上の写真の木工模型は中川さんが製作して下さいました。

大ピラミッド

エジプト・ギザの大ピラミッドは黄金比と白銀比に基づいています。一般に大ピラミッドは正四角錐形状であると信じられていますが、これは真実ではなく、実際は八面体形状です。この点は、ゴードン・マイケル・スキャリオン氏のベストセラー”Notes from the Cosmos”においても明らかにされています。これは、２つの合同な正四角錐が正方形の底面を共有するように結合された形です。これはまた、4枚の黄金菱形が短い対角線で山折りされ、各々の鋭角の頂点が共有されるように結合された立体でもあります。白銀比は、底面である正方形に内包されています。

研究成果

この分野における私の研究から、下記の事実が新たに見出されました。

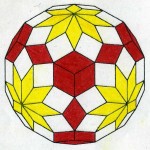
黄金比と白銀比は三次元において相互補完的な関係にある。右の写真が示すように、黄金化凸24面体（上）の凸部が白銀化凹60面体第1種（下）の凹部にピッタリ合わさっている。
黄金比と白銀二乗比は二次元において相互補完的な関係にある。
黄金菱形と白銀二乗菱形の組み合わせで平面充填が可能になる。
黄金比、黄金二乗比、白銀比および白銀二乗比に基づく螺旋は全部で６種類存在する。
白銀二乗長方形には無限の数の黄金長方形が含まれる。

これらの新発見はすべて論文にまとめられ、このホ－ムページに入っていますので、自由に参照することができます。

今後の課題

上記の特別の比４つは、高次元空間における立方体と密接な関係をもっているように思われます。その理由は下記の通りです。

４次元空間、6次元空間、10次元空間、１２次元空間における立方体をある特定の条件の下で３次元空間に投影すると、それぞれ、菱形１２面体、菱形３０面体、菱形９０面体、菱形１３２面体になる。
菱形１２面体は白銀菱形１２枚から構成される。
菱形３０面体は黄金菱形３０枚から構成される。
菱形９０面体は白銀菱形６０枚と黄金二乗菱形３０枚から構成される。

菱形１３２面体にはＴタイプとＣタイプの２種類があり、それぞれ３種類の菱形から構成されます。下記のスケッチを参照してください。上記の事実から、これらの３種類の菱形も白銀菱形、黄金菱形、黄金二乗菱形、あるいは白銀二乗菱形のどれかになるものと類推されます。しかし、この点はまだ確認されていません。また、次の点は今でも解明されておらず、謎に包まれています。